Publish Date: 2021-04-06

做法: 分类总结刷

时间复杂度

常见的时间复杂度

时间复杂度：评估执行程序所需的时间。可以估算出程序对处理器的使用程度

O(1)

执行常数次，和输入无关

def O1(num):
    i = num
    j = num*2
    return i+j

O(N)

def ON(num):
    total = 0
    for i in range(num):
        total+=i
    return total

一般来说有for循环基本是O(N) 但是这时候有个特例

let i =0; while(i<n)

这里也是O(N)

O(logN)

def OlogN(num);
     i = 1
     while(i < num):
         i = i*2
    return i

可以看出上面的代码，随着number每次乘以2后，都会越来越接近n，当number不小于n时就会退出循环。假设循环的次数为X，则由2^x=n得出x=log₂n，因此得出这个算法的时间复杂度为O(logn)。

O(M+N)

def OMN(num):
    total = 0
    for i in range(num):
        total += 1
    for j in range(num):
        total += j
    return total

O(NlogN)

def ONlogN(num1, num2):
    total = 0
    j = 0
    for i in range(num1):
        while(j < num2):
            total += i + j
            j = j*2
    return total

只要排序基本都是Nlog(N)

O(N^2)

for循环嵌套 While循环

def ON2(num):
    total = 0
    for i in range(num):
        for j in range(num):
            total += i + j
    return total

**这里很多时候以为嵌套的，就都是O(N^2)**内层循环的时间复杂度在讲到线性阶时就已经得知是O(n)，现在经过外层循环n次，那么这段算法的时间复杂度则为O(n²)。

但是下面这个并不是！！！！注意：因为他并不是从0开始的

for(int i=0;i<n;i++){   
      for(int j=i;j<n;i++){
         //复杂度为O(1)的算法
         ... 
      }
  }

需要注意的是内循环中int j=i，而不是int j=0。当i=0时，内循环执行了n次；i=1时内循环执行了n-1次，当i=n-1时执行了1次，我们可以推算出总的执行次数为：

n+(n-1)+(n-2)+(n-3)+……+1
=(n+1)+[(n-1)+2]+[(n-2)+3]+[(n-3)+4]+……
=(n+1)+(n+1)+(n+1)+(n+1)+……
=(n+1)n/2
=n(n+1)/2
=n²/2+n/2

根据此前讲过的推导大O阶的规则的第二条：只保留最高阶，因此保留n²/2。根据第三条去掉和这个项的常数，则去掉1/2,最终这段代码的时间复杂度为O(n²)。

其他常见复杂度

除了常数阶、线性阶、平方阶、对数阶，还有如下时间复杂度：
f(n)=nlogn时，时间复杂度为O(nlogn)，可以称为nlogn阶。
f(n)=n³时，时间复杂度为O(n³)，可以称为立方阶。
f(n)=2ⁿ时，时间复杂度为O(2ⁿ)，可以称为指数阶。
f(n)=n!时，时间复杂度为O(n!)，可以称为阶乘阶。
f(n)=(√n时，时间复杂度为O(√n)，可以称为平方根阶。

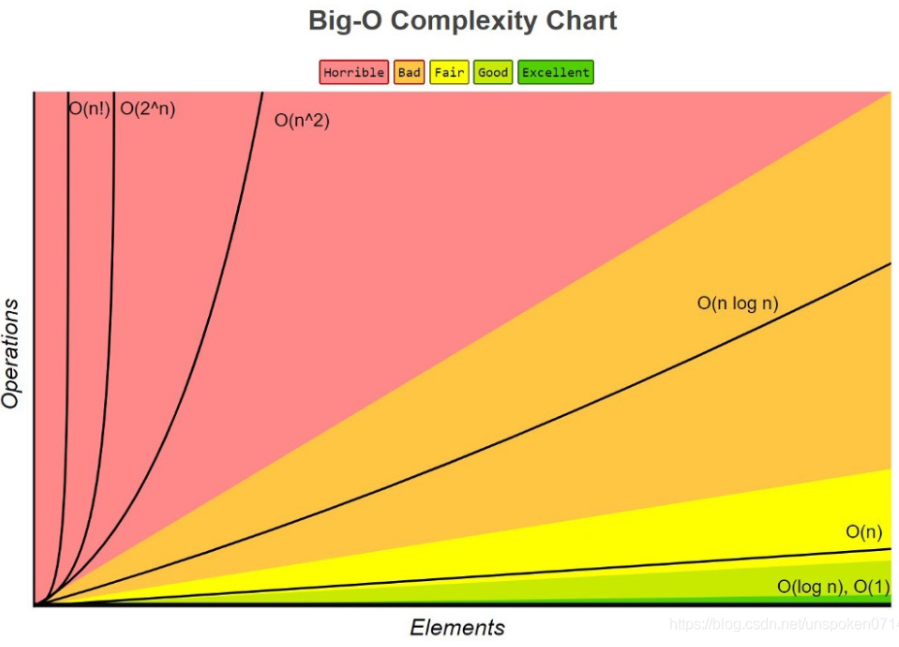
O(1) < O(logN) (二分查找) < O(N) < O(NlogN) < O(N^2) < O(2^n) < O(n!)

常见的空间复杂度

空间复杂度：评估执行程序所需的存储空间。可以估算出程序对计算机内存的使用程度。
O(1) < O(N) < O(N^2)

常量看其与输入值得关系
递归要考虑递归栈

O(1)

def ON(num):
    sum = 0;
    for i in range(num):
        sum = sum+i
    return sum

这里的占据的空间是固定的，没有根据输入值的改变而改变的

O(N)

def test(nums):
    array=[]
     for num in nums:
        array.append(num)
     return array

一个数占4个字节，所以array的空间与nums成正比；

例如 linked List array hashMap…

我们常见的空间复杂度就是O(1)、O(n)、 O(n2), 像O(logn)、O(nlogn) 这样的对数阶复杂度平时都用不到。而且，空间复杂度分析比时间复杂度分析要简单很多。

注意特殊：递归

由于数据会一直被存在stack中

O（N）

def ON(num):
    if(num<=0):
        return 0
    return ON(num-1) + ON(num-2)

复杂度分析的4个概念

最坏情况时间复杂度：代码在最坏情况下执行的时间复杂度。
最好情况时间复杂度：代码在最理想情况下执行的时间复杂度。
平均时间复杂度：代码在所有情况下执行的次数的加权平均值。
均摊时间复杂度：在代码执行的所有复杂度情况中绝大部分是低级别的复杂度，个别情况是高级别复杂度且发生具有时序关系时，可以将个别高级别复杂度均摊到低级别复杂度上。基本上均摊结果就等于低级别复杂度。

优化方法

数据结构

1. 数组

线性表: 线性表就是数据排成像一条线一样的结构.每个现行表上的数据最多只有前和后两个方向.常见的线性表结构：数组，链表、队列、栈等。

优点：两限制使得具有随机访问的特性缺点：删除，插入数据效率低

数组的搜索：找到这个元素对应的索引

复杂度

低效的插入和删除
1）插入：从最好O(1) 最坏O(n) 平均O(n)
2）插入：数组若无序，插入新的元素时，可以将第K个位置元素移动到数组末尾，把心的元素，插入到第k个位置，此处复杂度为O(1)。
3）删除：从最好O(1) 最坏O(n) 平均O(n)
4）多次删除集中在一起，提高删除效率

特点

适合读
不适合频繁做增删操作。
场景：读多写少

2. 链表

和数组一样，链表也是一种线性表。
从内存结构来看，链表的内存结构是不连续的内存空间，是将一组零散的内存块串联起来，从而进行数据存储的数据结构。
链表中的每一个内存块被称为节点Node。节点除了存储数据外，还需记录链上下一个节点的地址，即后继指针next

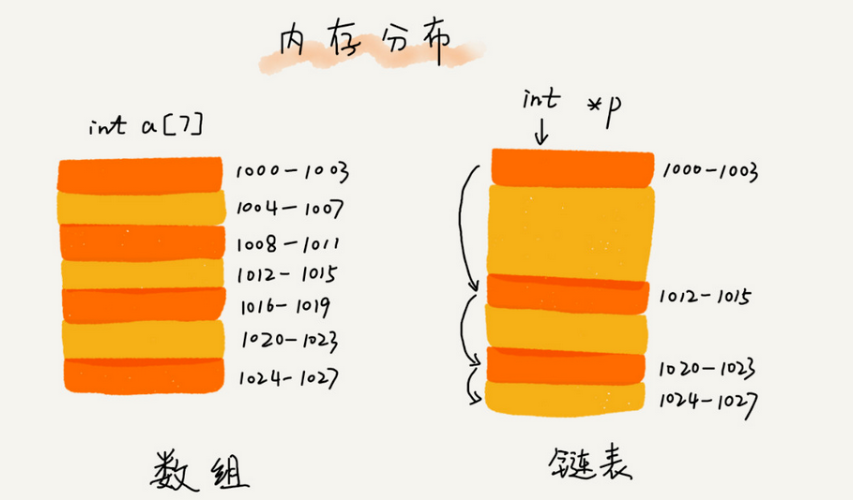
链表的特点

插入、删除数据效率高O(1)级别（只需更改指针指向即可），随机访问效率低O(n)级别（需要从链头至链尾进行遍历）。
和数组相比，内存空间消耗更大，因为每个存储数据的节点都需要额外的空间存储后继指针

常见列表

单列表(单行)

1）每个节点只包含一个指针，即后继指针。
2）单链表有两个特殊的节点，即首节点和尾节点。为什么特殊？用首节点地址表示整条链表，尾节点的后继指针指向空地址null。
3）性能特点：插入和删除节点的时间复杂度为O（1），查找的时间复杂度为O(n)。
循环链表

1）除了尾节点的后继指针指向首节点的地址外均与单链表一致。
2）适用于存储有循环特点的数据，比如约瑟夫问题。
双向列表

1）节点除了存储数据外，还有两个指针分别指向前一个节点地址（前驱指针prev）和下一个节点地址（后继指针next）。
2）首节点的前驱指针prev和尾节点的后继指针均指向空地址。
双向循环链表

选择数组还是链表？

1.插入、删除和随机访问的时间复杂度
数组：插入、删除的时间复杂度是O(n)，随机访问的时间复杂度是O(1)。
链表：插入、删除的时间复杂度是O(1)，随机访问的时间复杂端是O(n)。

淘汰策略

常见的3种包括先进先出策略FIFO（First In，First Out）、最少使用策略LFU（Least Frenquently Used）、最近最少使用策略LRU（Least Recently Used）。

3. 队列 queue

队列是一种受限的线性表数据结构,只支持两个操作:入栈push()和出栈pop0,队列跟非常相似,支持的操作也 ,很有限,最基本的操作也是两个:入队enqueue(),放一个数据到队列尾部;出队dequeue0),从队列头部取一个元素。

特点

队列跟栈一样,也是一种抽象的数据结构。
具有先进先出的特性,支持在队尾插入元素,在队头删除元素。

4. 栈 Stack

先进后出
基于链表创建的

单端队列：一个口进一个口出

双端队列：两个口都可以进，两个口都可以出

复杂度

访问: O(N)
搜索：O(N)
插入: O(1)
删除： O(1)

基本操作

function Stack(){
    //定义栈中的属性
    this.items = [];
    //栈的操作
    //1.元素入栈
    Stack.prototype.push = function (ele) {
        this.items.push(ele);
    }
    //2.取出栈顶元素（并返回）
    Stack.prototype.pop = function () {
        return this.items.pop();
    }
    //3.查看栈顶元素（返回）
    Stack.prototype.peek = function () {
        return this.items[this.items.length - 1];
    }
    //4.判断栈是否为空
    Stack.prototype.isEmpty = function () {
        return this.items.length == 0;
    }
    //5.获取栈中元素的个数
    Stack.prototype.size = function () {
        return this.items.length;
    }
    //6.toString方法
    Stack.prototype.toString = function () {
        var resultString = '';
        for( var i =0; i < this.items.length ; i++){
            resultString += this.items[i] + ' ';
        }
        return resultString;
    }
}

5. 哈希表

哈希表是基于数组实现的，数组相对的劣势有：

插入和删除效率低；

基于内容查找效率也不高；

哈希表的优势 :

提供快速的插入-删除-查找操作
O(1)的时间级，只需要几个机器指令完成；
速度比树还快，编码更容易。

哈希表的劣势：

数据是没有顺序的，不能用特定顺序的方式遍历元素；
哈希表的key不能重复。

排序

前言

（1）几种最经典、最常用的排序方法：冒泡排序、插入排序、选择排序、快速排序、归并排序、计数排序、基数排序、桶排序。

（2）复杂度归类

冒泡排序、插入排序、选择排序 O(n^2)
快速排序、归并排序 O(nlogn)
计数排序、基数排序、桶排序 O(n)

原地排序算法：特指空间复杂度是O(1)的排序算法。

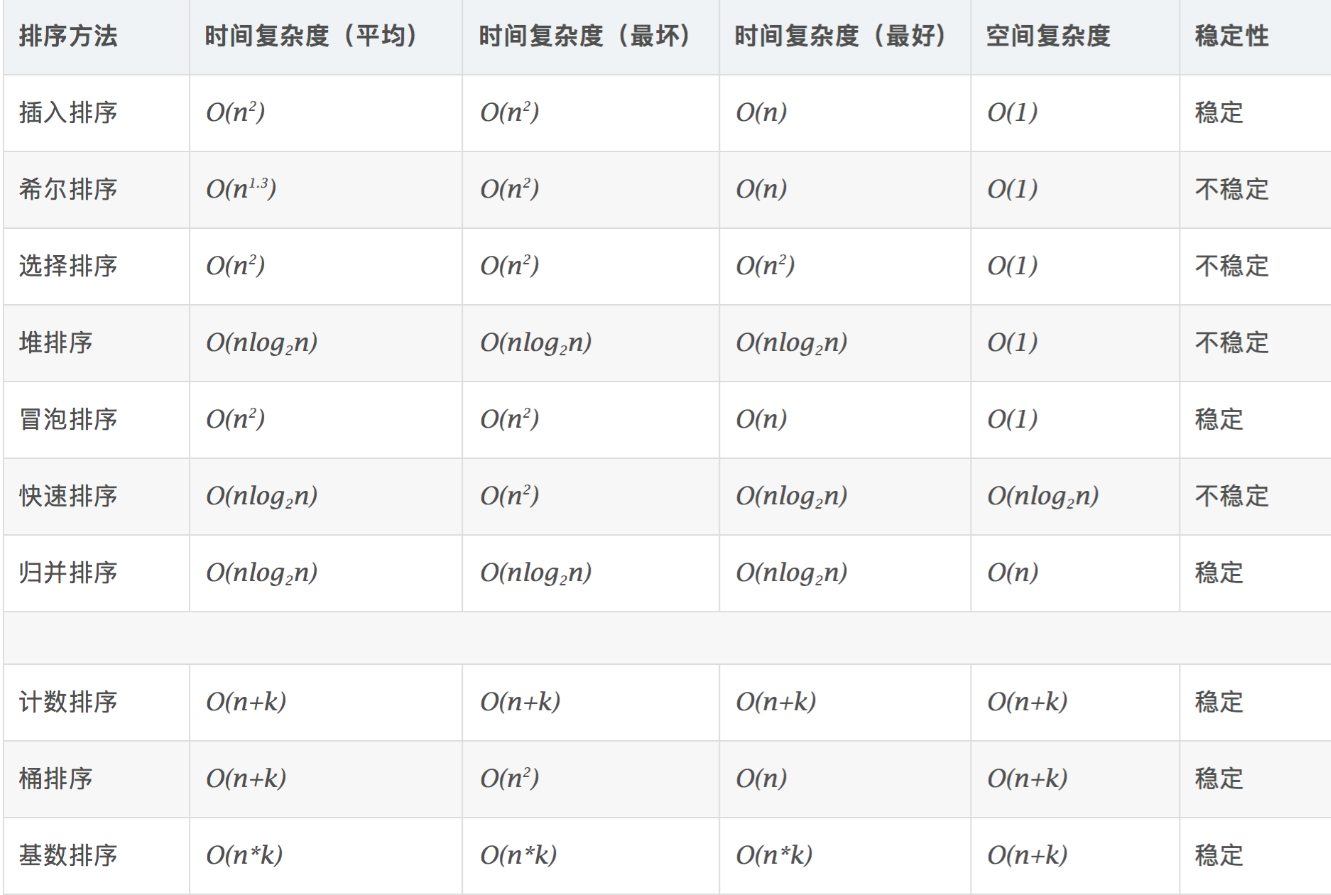
冒泡排序,插入排序,选择排序

冒泡排序

相当于把最大的一直推到最后

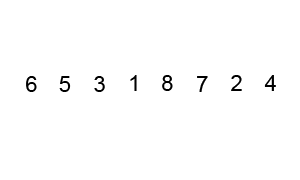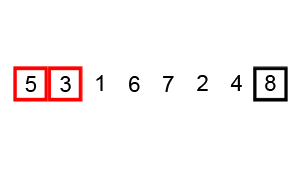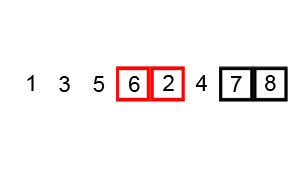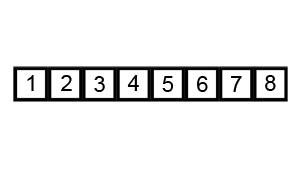
const bubbleSort = (array) => {
    // 不修改原数组
    const originValues = array.slice(); 
    // 迭代次数 数组长度-1
    for (let i = 0; i < originValues.length - 1; i++) {
        // 两两比较，该迭代的最大数，移动到右侧相应位置
        for (let j = 0; j < originValues.length - 1 - i; j++) {
            // 如果前一个数，大于后一个数，交换
            if (originValues[j] > originValues[j + 1]) {
                const tmp = originValues[j];
                originValues[j] = originValues[j + 1];
                originValues[j + 1] = tmp;
            }
        }
    }
    return originValues;
};

function optimzedBubbleSort = (arr) => {
  const  n = arr.length;
  let swapped = true;

  // 一共要跑 n 輪
  for (let i = 0; i < n && swapped; i++) {

    // 從第一個元素開始，不斷跑到第 n - 1 - i 個
    // 原本是 n - 1，會再加上 - i 是因為最後 i 個元素已經排好了
    // 所以沒必要跟那些排好的元素比較
    swapped = false;
    for (let j = 0; j < n - 1 - i; j++) {
      if (arr[j] > arr[j + 1]) {
        swapped = true;
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
      }
    }
  }
  return arr;
}

改良之後，如果輸入是已經排好的陣列，就只會跑一次內圈，然後就跳掉了，所以時間複雜度會是O(n)

插入排序

第一个基本固定,后面的通过与第一个对比,进行排序

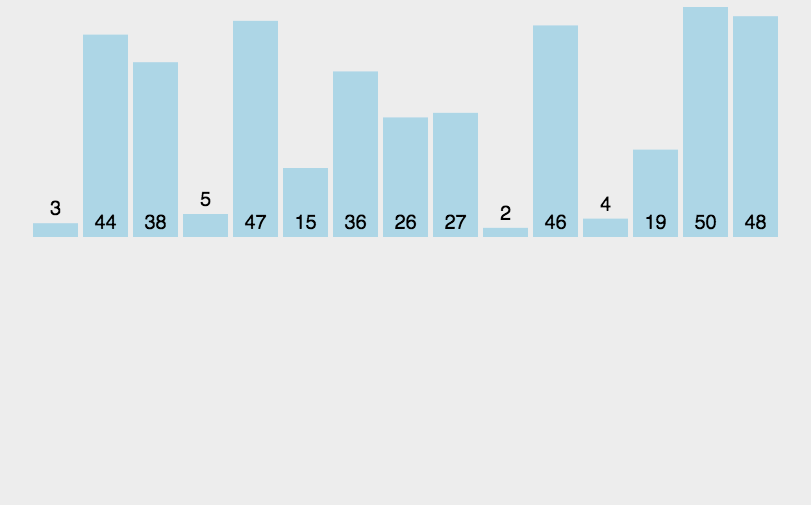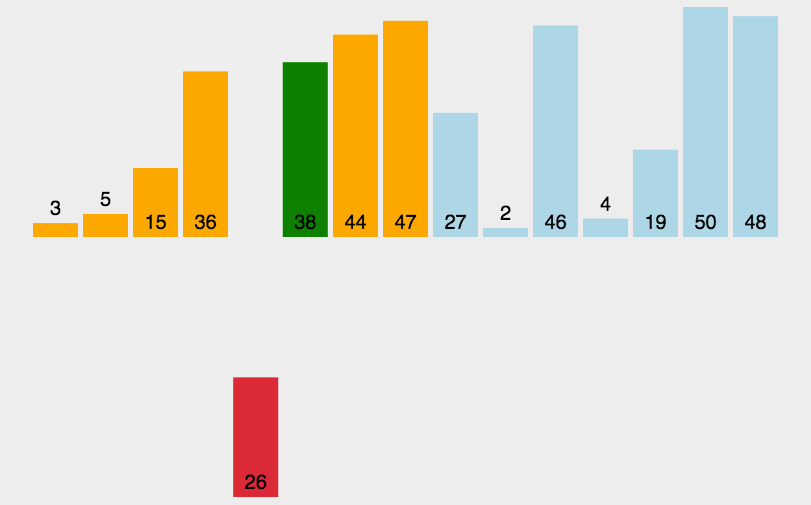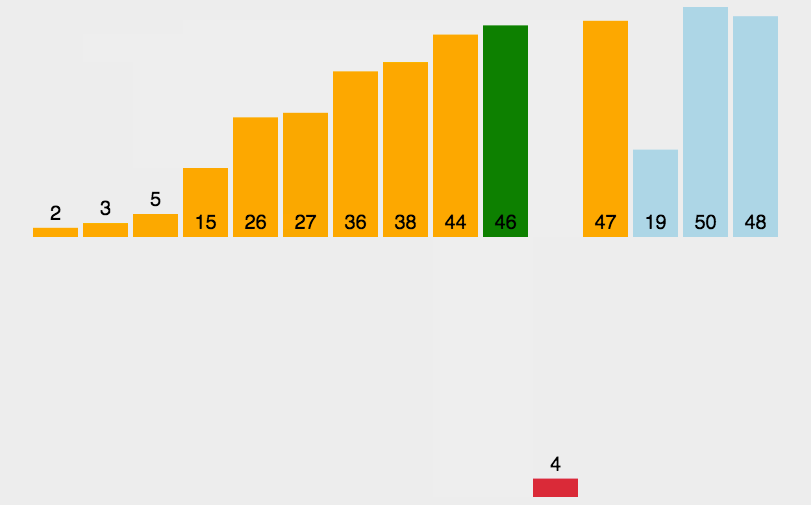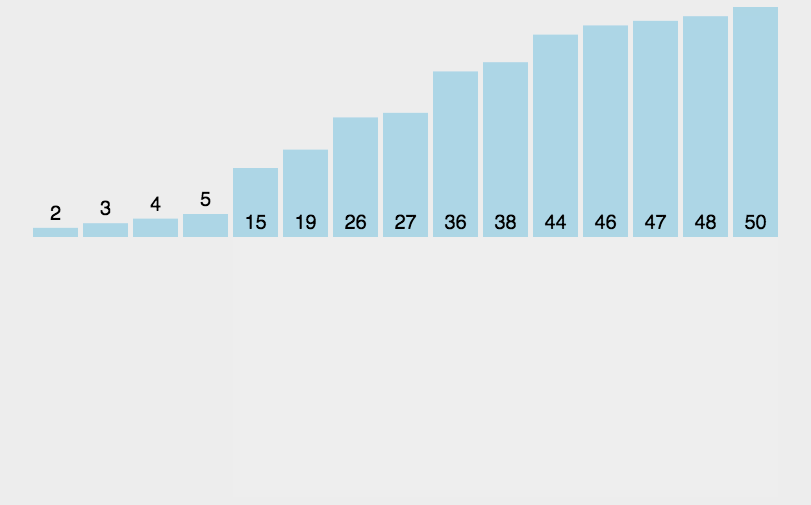
Insertion Sort

function insertSort(arr) {
  // 缓存数组长度
  const len = arr.length
  // temp 用来保存当前需要插入的元素
  let temp  
  // i用于标识每次被插入的元素的索引
  for(let i = 1;i < len; i++) {
    // j用于帮助 temp 寻找自己应该有的定位
    let j = i
    temp = arr[i]  
    // 判断 j 前面一个元素是否比 temp 大
    while(j > 0 && arr[j-1] > temp) {
      // 如果是，则将 j 前面的一个元素后移一位，为 temp 让出位置
      arr[j] = arr[j-1]   
      j--
    }
    // 循环让位，最后得到的 j 就是 temp 的正确索引
    arr[j] = temp
  }
  return arr
}
var arr = [4, 2, 1, 3];
insertionSort(arr); //[1, 2, 3, 4]

选择排序 selectionSort

找到最小排前面

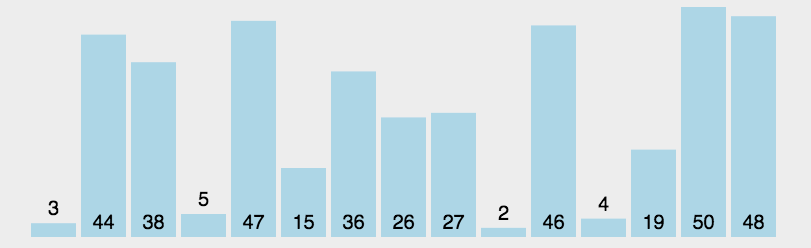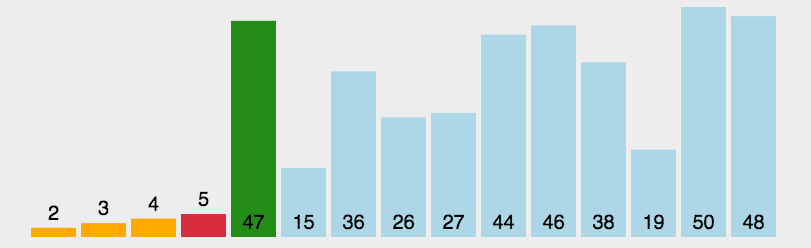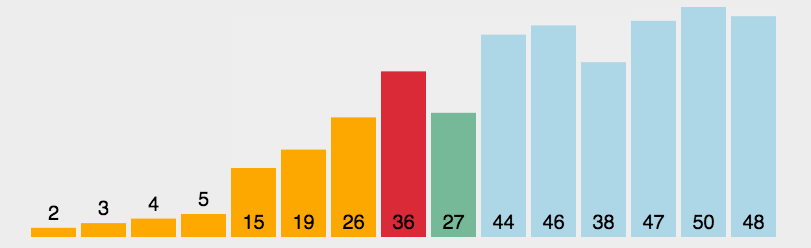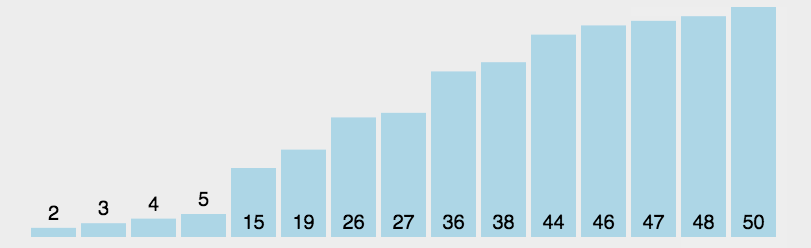
选择排序（Selection Sort）

function selectSort(arr)  {
  // 缓存数组长度
  const len = arr.length 
  // 定义 minIndex，缓存当前区间最小值的索引，注意是索引
  let minIndex  
  // i 是当前排序区间的起点
  for(let i = 0; i < len - 1; i++) { 
    // 初始化 minIndex 为当前区间第一个元素
    minIndex = i  
    // i、j分别定义当前区间的上下界，i是左边界，j是右边界
    for(let j = i; j < len; j++) {  
      // 若 j 处的数据项比当前最小值还要小，则更新最小值索引为 j
      if(arr[j] < arr[minIndex]) {  
        minIndex = j
      }
    }
    // 如果 minIndex 对应元素不是目前的头部元素，则交换两者
    if(minIndex !== i) {
      [arr[i], arr[minIndex]] = [arr[minIndex], arr[i]]
    }
  }
  return arr
}

高级排序快速排序,归并排序

归并排序 mergeSort

该算法是采用分治法（Divide and Conquer）的一个非常典型的应用

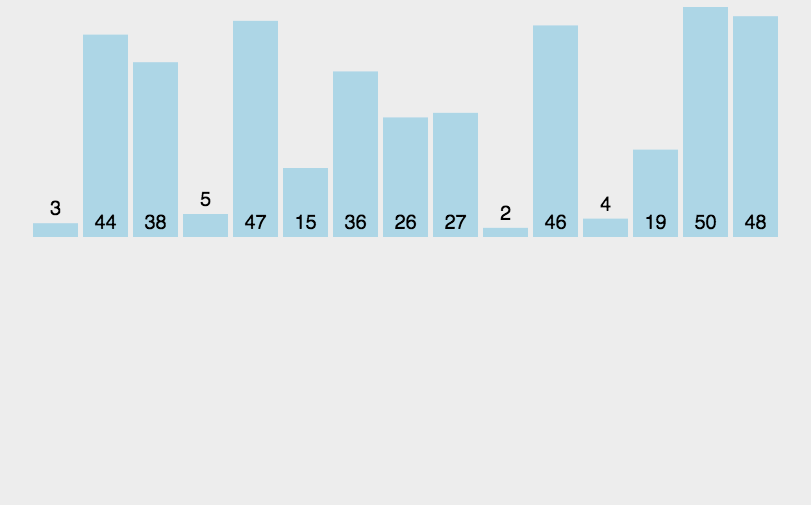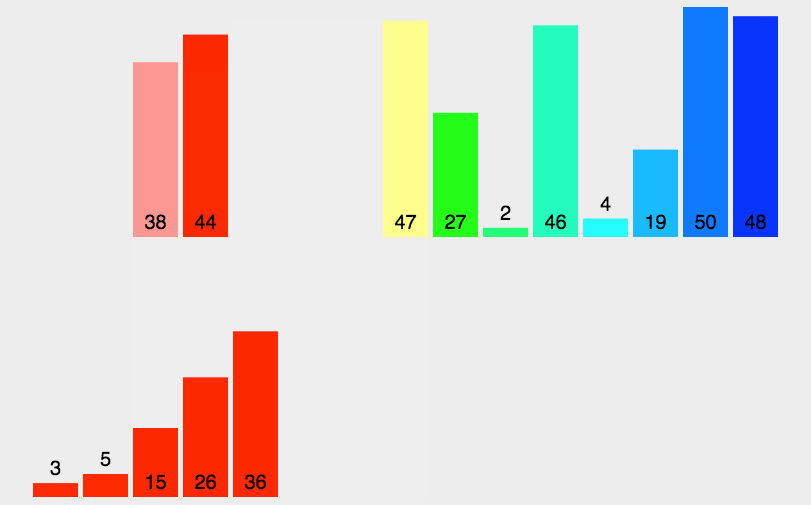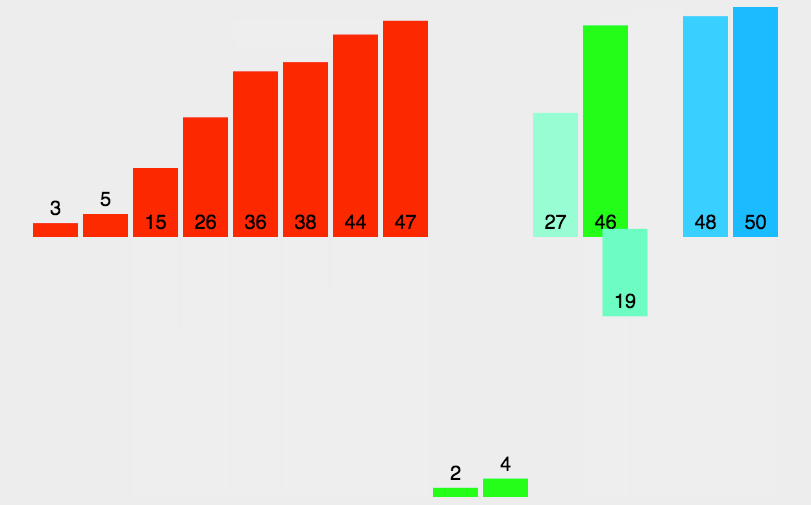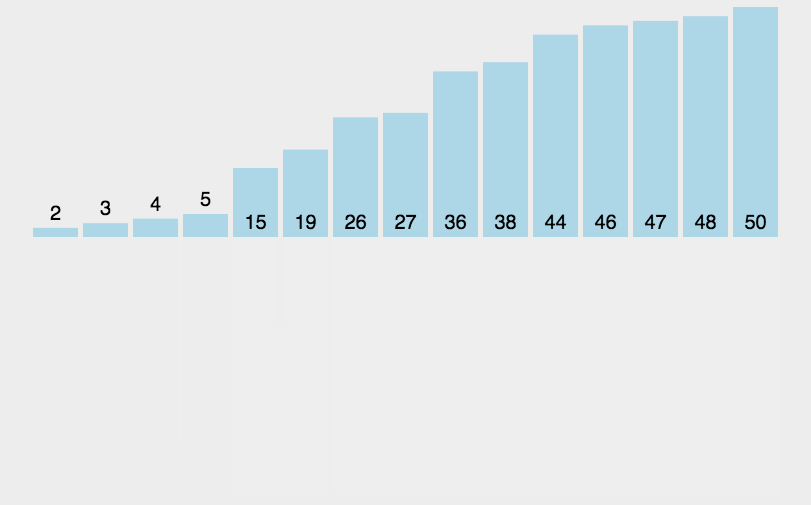
归并排序（Merge Sort）

const simpleMergeSort = (arr) => {

  // 合併
  const merge = (leftArray, rightArray) => {
    let result = [];
    let nowIndex = 0, left = 0, right = 0;
    const leftLength = leftArray.length;
    const rightLength = rightArray.length;

    // 如果左右兩邊都沒抓完，就看誰比較小抓誰
    while (left < leftLength && right < rightLength) {
      if (leftArray[left] < rightArray[right]) {
        result[nowIndex++] = leftArray[left++];
      } else {
        result[nowIndex++] = rightArray[right++];
      }
    }

    // 跑到這裡代表左右兩邊其中一邊抓完了
    // 如果是左邊沒抓完，全部抓下來
    while (left < leftLength) {
      result[nowIndex++] = leftArray[left++];
    }

    // 右邊沒抓完，全部抓下來
    while (right < rightLength) {
      result[nowIndex++] = rightArray[right++];
    }

    // 把合併好的陣列直接傳回去
    return result;
  }
  const _mergeSort = (arr) => {
    const length = arr.length;
    if (length <= 1) return arr;

    // 切兩半
    const middle = Math.floor(length / 2);

    // 排左邊
    const leftArray = _mergeSort(arr.slice(0, middle));

    // 排右邊
    const rightArray = _mergeSort(arr.slice(middle, length));

    // 合併後丟回去
    return merge(leftArray, rightArray);
  }
  return _mergeSort(arr);
}

快速排序 quickSort

找一個數，並且把這個數調整到：讓左邊的元素比它小，右邊的元素比它大，再對左右兩遍做一樣的事

function quickSort(arr) {
    if (arr.length <= 1) { // 如果数组长度小于等于1无需判断直接返回即可
      return arr;
    }
    var pivotIndex = Math.floor(arr.length / 2); // 取基准点
    var pivot = arr.splice(pivotIndex, 1)[0]; // 取基准点的值,splice(index,1)函数可以返回数组中被删除的那个数
    var left = []; // 存放比基准点小的数组
    var right = []; // 存放比基准点大的数组
    for (var i = 0; i < arr.length; i++) {  // 遍历数组，进行判断分配
      if (arr[i] < pivot) {
        left.push(arr[i]); // 比基准点小的放在左边数组
      } else {
        right.push(arr[i]); // 比基准点大的放在右边数组
      }
    }
    //递归执行以上操作,对左右两个数组进行操作，直到数组长度为<=1；
    return quickSort(left).concat([pivot], quickSort(right));
  };
  var arr = [1, 2, 3, 55, 7, 99, 8, 100, 1021];
  var sortedArr = quickSort(arr);
  console.log(sortedArr);

十大经典排序算法（动图演示）

推荐对于算法可视化的网站

Savannah

http://savancode.github.io

All articles in this blog are used except for special statements CC BY 4.0 reprint polocy. If reproduced, please indicate source Savannah !

JS alog

JS 高级程序设计重点摘抄以及解读2

JS 高级程序设计中函数以及函数作用域 this 闭包

2021-04-07 JS

JS book this

js working principle JS引擎工作原理

JS引擎工作原理

2021-04-06 JS

js 基础算法 十大经典排序算法（动图演示）

时间复杂度

常见的时间复杂度

O(1)

O(N)

O(logN)

O(M+N)

O(NlogN)

O(N^2)

其他常见复杂度

常见的空间复杂度

O(1)

O(N)

注意特殊：递归

复杂度分析的4个概念

优化方法

数据结构

1. 数组

复杂度

特点

2. 链表

链表的特点

常见列表

选择数组还是链表？

淘汰策略

3. 队列 queue

特点

4. 栈 Stack

复杂度

基本操作

5. 哈希表

排序

前言

冒泡排序,插入排序,选择排序

冒泡排序

插入排序

选择排序 selectionSort

高级排序 快速排序,归并排序

归并排序 mergeSort

快速排序 quickSort

十大经典排序算法（动图演示）

js 基础算法十大经典排序算法（动图演示）

高级排序快速排序,归并排序